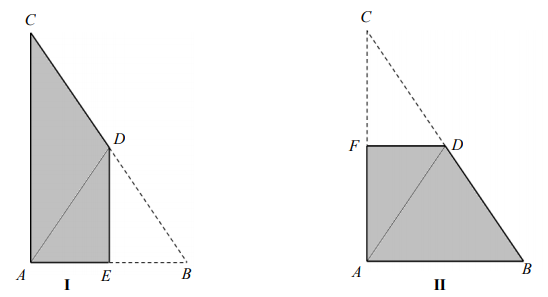
Pole czworokąta I jest równe polu czworokąta II. Obwód czworokąta I jest mniejszy od obwodu czworokąta II.
Ania wycięła z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 12 cm, 16 cm i 20 cm. Pierwszy z nich zagięła wzdłuż symetralnej krótszej przyprostokątnej, a drugi – wzdłuż symetralnej dłuższej przyprostokątnej. W ten sposób otrzymała czworokąty
pokazane na rysunkach.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.

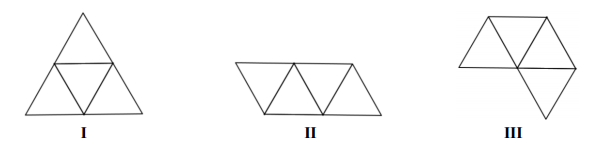
Które wielokąty – I, II, III – przedstawiają siatki bryły takiej, jaką pokazano na powyższych rysunkach?
Rysunki przedstawiają bryłę, której wszystkie cztery ściany są trójkątami równobocznymi.

Które wielokąty – I, II, III – przedstawiają siatki bryły takiej, jaką pokazano na powyższych rysunkach? Wybierz właściwą odpowiedź spośród podanych.
A. I, II i III
B. tylko I i III
C. tylko II i III
D. tylko I i II
Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości...
Szklane naczynie w kształcie prostopadłościanu o wymiarach 6 cm, 15 cm i 18 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 4 cm.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A. 8 cm
B. 10 cm
C. 12 cm
D. 16 cm
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa 36 cm3.
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa 36 cm3.
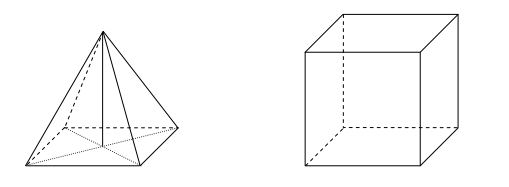
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.

Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego?
Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego? Zapisz obliczenia i odpowiedź.
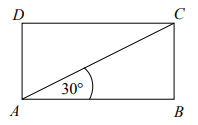
Przekątna prostokąta ABCD nachylona jest do jednego z jego boków pod kątem 30°. Uzasadnij, że pole prostokąta ABCD jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
Przekątna prostokąta ABCD nachylona jest do jednego z jego boków pod kątem 30°. Uzasadnij, że pole prostokąta ABCD jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
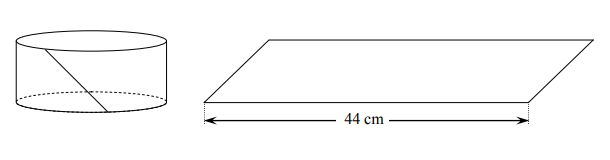
Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 44 cm, a jej pole jest równe 220 cm2. Oblicz objętość tego pudełka.
Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 44 cm, a jej pole jest równe 220 cm2. Oblicz objętość tego pudełka. Przyjmij przybliżenie π równe 22/7. Zapisz
obliczenia.