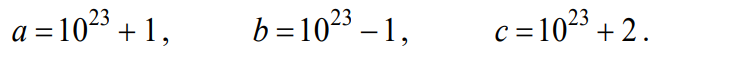DWMED

Do zbiornika wypełnionego w 65% wodą dolano 12 litrów wody. Teraz woda wypełnia 80%
pojemności zbiornika.

Ile litrów wody jest teraz w zbiorniku? Wybierz właściwą odpowiedź spośród podanych.

A. 52 litry

B. 64 litry

C. 77 litrów

D. 80 litrów

Dane są trzy liczby:

Które z tych liczb są podzielne przez 3? Wybierz właściwą odpowiedź spośród podanych.

A. Tylko liczby a i b.
B. Tylko liczba b.
C. Tylko liczby b i c.
D. Tylko liczba c.

Dany jest zestaw liczb: 4, 9, 11, 15, 21.

Do podanych liczb dopisano jeszcze jedną liczbę i wtedy średnia arytmetyczna nowego zestawu liczb zwiększyła się o 1.

Która liczba została dopisana? Wybierz właściwą odpowiedź spośród podanych.

A. 10

B. 12

C. 13

D. 18

W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów
równoramiennych, jak przedstawiono na rysunku 1.

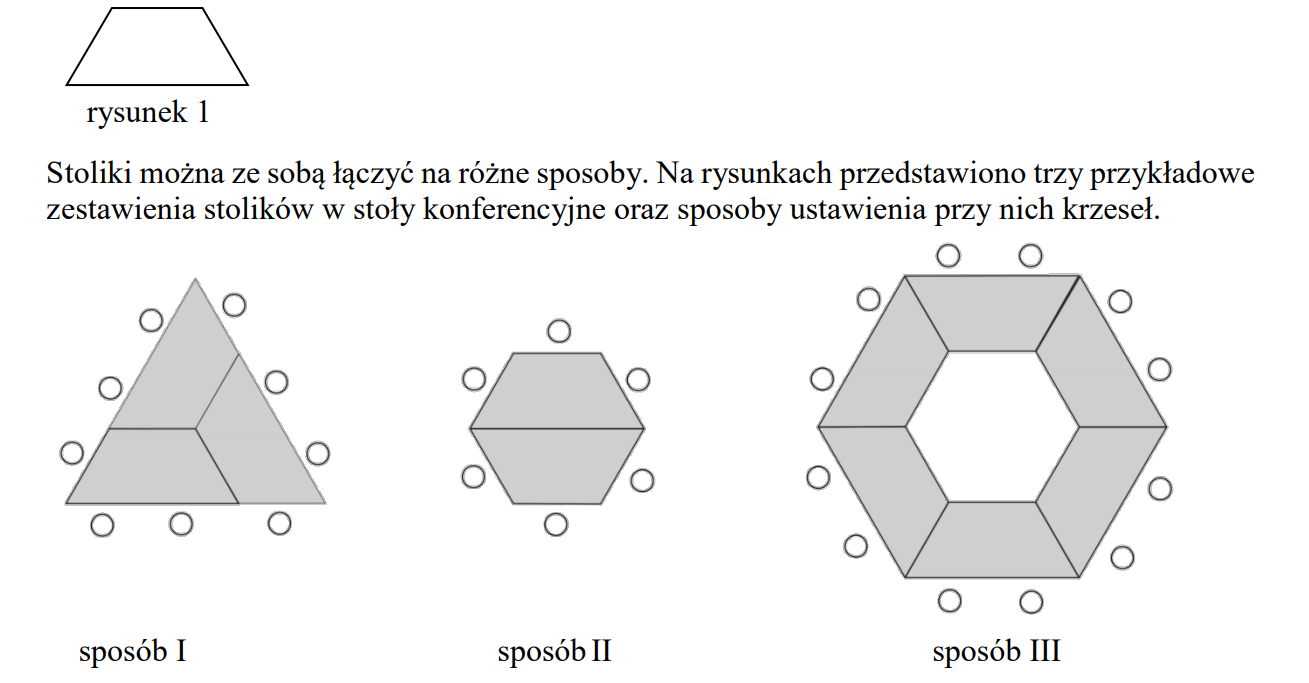
W ośrodku jest 36 stolików. Postanowiono je ustawić w jeden z trzech sposobów pokazanych na powyższych rysunkach.

Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.

A. Po ustawieniu wszystkich stolików w sposób I uzyska się tyle samo miejsc siedzących, ile
powstaje po ustawieniu wszystkich stolików w sposób II.
B. Najmniejszą liczbę miejsc siedzących uzyska się po ustawieniu wszystkich stolików
w sposób III.
C. Po ustawieniu wszystkich stolików w sposób I uzyska się 108 miejsc siedzących.
D. Po ustawieniu wszystkich stolików w sposób II uzyska się 96 miejsc siedzących.

W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów
równoramiennych, jak przedstawiono na rysunku 1.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

W układzie współrzędnych zaznaczono trzy punkty A, B, C o współrzędnych całkowitych, jak
na rysunku.

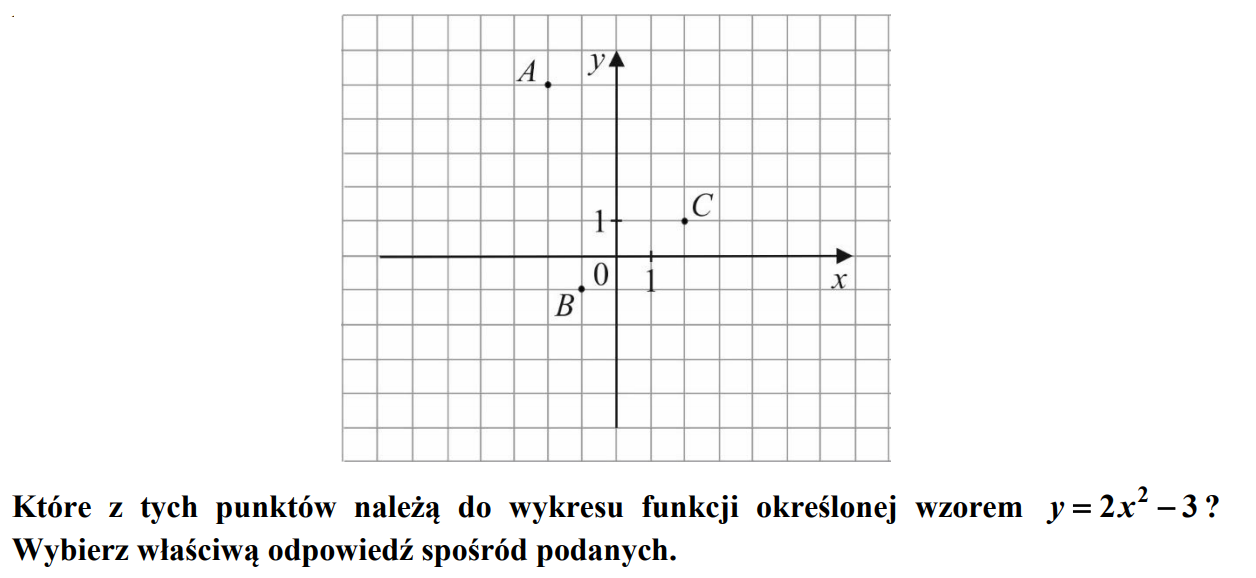
A. A, B i C.

B. Tylko A i C.

C. Tylko B i C.

D. Tylko A i B.

Czy 18% liczby 15 jest większe niż 15% liczby 18? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.

Punkty A i B są środkami boków kwadratu o polu

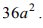
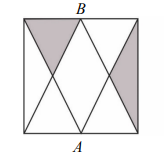
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Suma pól zacieniowanych części kwadratu jest równa

Na dwóch bokach trójkąta prostokątnego ABC zbudowano kwadraty. Pole kwadratu
zbudowanego na boku BC jest równe 169, a pole kwadratu zbudowanego na boku AC jest
równe 25.

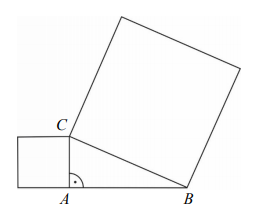
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.

Pole ćwiartki koła przedstawionej na rysunku jest równe

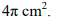
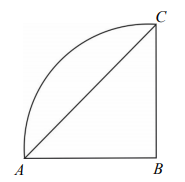
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole trójkąta ABC jest równe

Prostokątna ramka ma szerokość 2 cm oraz |KL| =15 cm, |NK| = 9 cm (patrz rysunek).

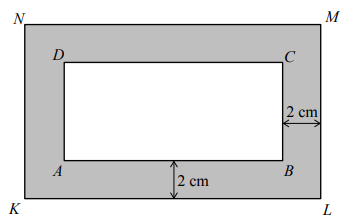
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.

Ostrosłup i graniastosłup mają takie same podstawy. Obie bryły mają łącznie 25 wierzchołków.

Ile wierzchołków ma ostrosłup? Wybierz właściwą odpowiedź spośród podanych.

A. 6

B. 8

C. 9

D. 10

Z sześcianu o objętości 27 cm3 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana
usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał
do krawędzi sześcianu.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole powierzchni powstałej bryły jest równe

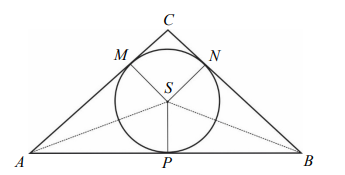
W trójkąt równoramienny ABC ( AC BC = ) wpisano okrąg o środku S. Punkty wspólne
okręgu i trójkąta oznaczono literami M, N i P. Uzasadnij, że trójkąty ASM i PBS są
przystające.

Na statku wycieczkowym są 33 miejsca dla pasażerów. Uczniowie klas IIIa i IIIb planują
wycieczkę tym statkiem. W każdej z tych klas jest mniej niż 33 uczniów. Aby wszystkie
miejsca dla pasażerów były na statku zajęte, należy do wszystkich uczniów klasy IIIa
dołączyć 1/3 uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć 1/4 uczniów
klasy IIIa. Ilu uczniów jest w każdej z tych klas? Zapisz obliczenia.