DWMED

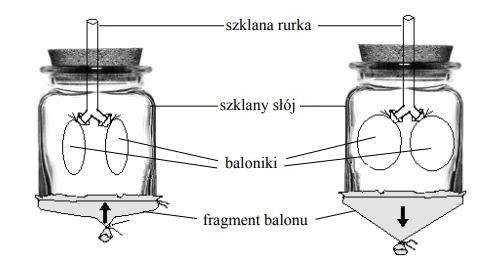
Na rysunku przedstawiono model klatki piersiowej, który uczniowie wykorzystali do
zilustrowania pewnego procesu.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Za pomocą tego modelu pokazano

A. współdziałanie żeber i mięśni klatki piersiowej podczas wdechu.
B. wymianę gazów oddechowych w płucach.
C. znaczenie przepony w wentylacji płuc.
D. wydawanie głosu.

Uczniowie badali wpływ różnych czynników na kiełkowanie nasion pewnej rośliny.
W tym celu przygotowali trzy zestawy z taką samą liczbą nasion i zapewnili im różne
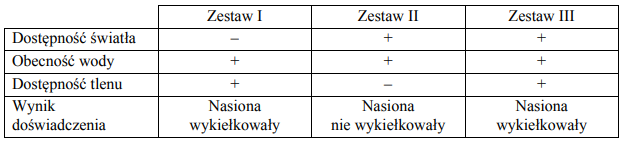
warunki. Dokumentację doświadczenia przedstawili w tabeli. Znakiem „+” zaznaczyli
obecność danego czynnika w zestawie doświadczalnym, a znakiem „–” brak czynnika
w zestawie. Zapisali też wynik doświadczenia.

Oceń prawdziwość podanych informacji. Wybierz P, jeśli informacja jest prawdziwa,
albo F – jeśli jest fałszywa.

Zaleszczotki żyją w ściółce leśnej, pod korą obumarłych drzew oraz w glebie. Mają ciało
podzielone na głowotułów i odwłok, cztery pary odnóży krocznych, gruczoły jadowe, a także
gruczoły przędne, które znajdują się na odnóżach gębowych. Zaleszczotki są też
pożytecznymi mieszkańcami uli, w których żywią się roztoczami szkodliwymi dla pszczół
i małymi gąsienicami owadów.

Uzupełnij zdanie. Wybierz właściwe odpowiedzi spośród podanych.

Zaleszczotki należą do A/B, ponieważ mają C/D.

A. pajęczaków

B. owadów

C. cztery pary odnóży krocznych

D. gruczoły jadowe

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F –
jeśli zdanie jest fałszywe.

Pojemnik z kremem ma kształt walca o promieniu podstawy 4 cm i wysokości 4,5 cm.
Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę
o promieniu 3 cm. Ile razy objętość tej półkuli jest mniejsza od objętości walca? Zapisz
obliczenia.

Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem.
W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym
przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów
pojechało na tę wycieczkę? Zapisz obliczenia.

Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 11,
wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej
piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka
jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.

Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: P, S, T, W, Z są środkami jego
krawędzi.

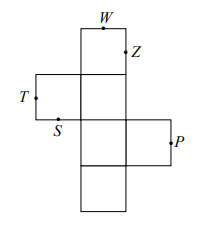
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Po złożeniu sześcianu z tej siatki punkt P pokryje się z punktem

A. W

B. Z

C. T

D. S

Każdy bok kwadratu ABCD podzielono na 3 równe części i połączono kolejno punkty
podziału, w wyniku czego otrzymano ośmiokąt (rysunek).

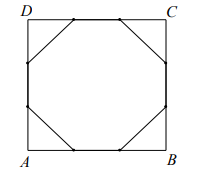
Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród
podanych.

A. Ośmiokąt jest foremny.
B. Wszystkie boki ośmiokąta mają taką samą długość.
C. Każdy kąt wewnętrzny ośmiokąta ma miarę 135°.
D. Obwód ośmiokąta jest większy od obwodu kwadratu ABCD.

Ewa narysowała kwadrat o boku 1, prostokąt o bokach 2 i 1 oraz kąt prosty o wierzchołku O.

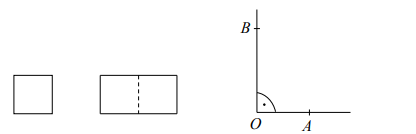
Następnie od wierzchołka O kąta prostego odmierzyła na jednym ramieniu kąta odcinek OA
o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek OB o długości równej
przekątnej prostokąta.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Długość odcinka AB jest równa

Punkty E i F są środkami boków BC i CD kwadratu ABCD (rysunek).

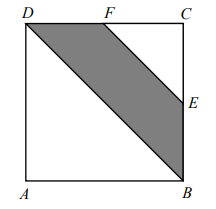
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
zdanie jest fałszywe.

Proste KA i KB są styczne do okręgu o środku S w punktach A i B, a kąt BMA ma miarę 42°
(rysunek).

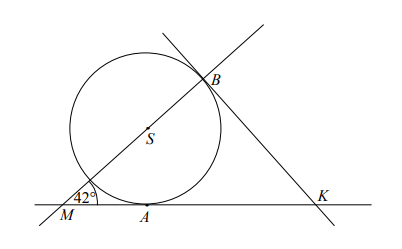
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Kąt AKB jest równy

A. 58°

B. 52°

C. 48°

D. 42°

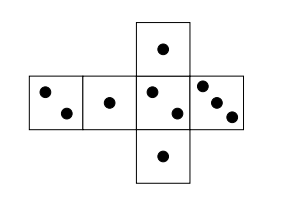
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz
taką kostką.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
zdanie jest fałszywe.

Kasia ma 6 lat. Średnia arytmetyczna wieku Ani i Pawła jest równa 12 lat.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Średnia arytmetyczna wieku Kasi, Ani i Pawła jest równa

A. 6 lat.

B. 9 lat.

C. 10 lat.

D. 15 lat.

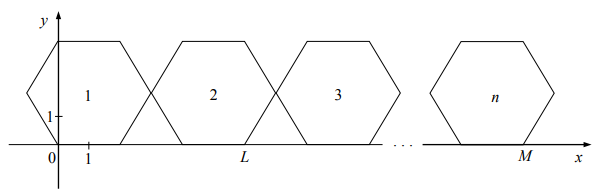
Do sześciokąta przedstawionego na rysunku w zadaniu 12. dorysowujemy kolejne takie same
sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał
z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta
leżał na osi x. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które
ponumerowano kolejnymi liczbami naturalnymi.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
zdanie jest fałszywe.

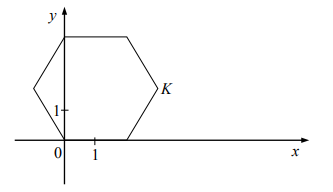
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego
wierzchołków jest punkt (0, 0), a jeden z jego boków leży na osi x (rysunek)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Współrzędne wierzchołka K tego sześciokąta są równe